Le MOMOSITE vous présente :
	LA SOLUCE DE 64-65
	Page mise à jour le 26/01/2010

Il est évident qu'il doit y avoir quelque chose qui cloche !
Les points S T U V ainsi que W et X sont pré-choisis donc de ce coté rien d'anormal !
Mais les point Z et Y ? Sont-ils vraiment à 3 unités respectives des points X et W ?

Le Dessin a l'air de dire Oui !

Mais les math ?

Notre rectangle fait 13 x 5 = 65 carrés. Donc la demi-surface (constitué d'un triangle et d'un trapèze) = 65/2 = 32,5 carrés

Vérifions en calculant les deux surfaces puis en les additionnant :
Mais avant, il nous faut vérifier que les points Z et Y sont vraiment 3 unités respectives des points X et W.

Nous allons donc attribuer la lettre a au segment WY et le déclarer inconnue

sachant que (triangle 1 + trapèze 1) = 32,5 carrés,

mettons tout ça en équation
(8a  ) / 2 + [(a + 5)/ 2 x 5)] = 32,5
4a + 2,5a + 12,5 = 32,5
6,5a = 20
a = 20 / 6,5
a = 3,077

verif :

Surface d'un Trapèze :
Moyenne des bases par hauteur
[(3,077+5)/2] x 5 = 20,19

Surface d'un Triangle :
(Base x hauteur) / 2
(3,077 x 8) / 2=12,31

1/2 Surface totale = 20,19 + 12,31 = 32,50
Surface totale = 32,50 x 2 = 65

En fait le problème est faussé au départ :
soit la ligne n'est pas droite, et inconsciemment on en corrige les défauts supposés
soit la ligne est trop épaisse et les 7,7 % de marge d'erreur passent inaperçu !
Quand à la preuve par le découpage, là encore, tout cela est rarement droit... et puis surtout on a changé les propriétés du quadrilatère qui est devenu un carré parfait, or un découpage à l'exacte des quatre figures ne permettrait pas de l'obtenir

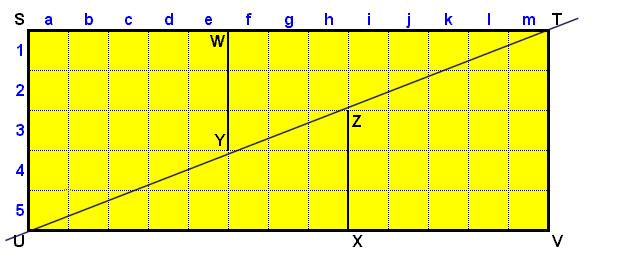
Sur cette figure agrandie on voit bien que les points Y et Z ne sont pas sur la diagonale UT ! (Y est à 0,077 carrés de la diagonale. Idem pour Z .